Genetic Algorithms

Have been reading about genetic algorithms (GA) from here, an awesome website which provides an introduction to the concept without assuming a deep knowledge of eitheir biology nor programming. GA seems really useful and have to study some more examples (apart from the travelling salesman problem) to digest the idea completely.

Debugging ideas for the scheduler project

1) An entry in the proc file system which will show the current tasks on the current runqueue
2) An entry in the proc file system which will illustrate the tasks in the new runqueue structure

Parts of the project

0) Changing HZ to 1000 in the include/asm-um/param.h
1) Implementing sleeping average for the process in the 2.4 kernel. This will then be used to calculated the new dynamic priority and timeslices.
2) Adding the data structures and associated functions for the enchanced runqueue and
3) Finally modifying the scheduling code.

o(1) scheduler for 2.4.30 kernel

Earlier this year I had started working on porting the 0(1) process scheduler from the 2.6 Linux kernel to the 2.4 kernel. However I never completed the project since I got occupied with lots of other things. Now I plan to get back to it and am hoping to complete it this time. The reason I am working on this project is that I don't want to loose touch with kernel programming. Currently I am not doing much of system level programming, however I would like to keep sharping my skills everyday. Also I won't be able to release this patch when (hopefully I will) I get done due to my current job restrictions but that's cool since they pay me.

Any I have learnt a few this from my previous attempt towards this task

1) Always break a big task into number of smaller logical tasks. These will then form the building blocks of the entire task.
2) Read, read and read lots of documentation
3) Try learning new tools. For example, I think I have improved my gdb skills a lot as compared to the start of this year. This is going to help me a lot in debugging this project
4) Don't be afraid of trying out new things and experiment. Sometimes knowledge does limit your thinking.

Avoid being bugged by SIGUSR1 in UML

Inorder to prevent being bugged by the SIGUSR1 in UML (User Mode Linux), set the following two options in gdb

(host gdb) handle SIGSEGV pass nostop noprint

(host gdb) handle SIGUSR1 pass nostop noprint

Important features of the 2.4 process scheduler

I am reading the book process scheduling chapter from the "Understanding the Linux kernel" book. Following are some of the important points about the 2.4 kernel scheduler.

1) Process scheduling in Linux is Time Shared.
2) Processes are preemptive in the 2.4 Linux kernel.
3) The need_resched flag is set whenever the time quantum assigned to the process expires.
4) The 2.4 kernel is non-preemptive i.e. a process can be preempted only when it is executing in the User mode and canNOT be preempted when the process is running in the kernel mode.

Valid Peg Puzzle Solution

00000000000000000111111111111110
00000000000000000111111111110101
00000000000000000111111111001101
00000000000000000111111111101000
00000000000000000111111110100010
00000000000000000111110110000110
00000000000000000111010100010110
00000000000000000110010000110110
00000000000000000110010100100100
00000000000000000110011100000000
00000000000000000010010100100000
00000000000000000011010000000000
00000000000000000000110000000000
00000000000000000001000000000000

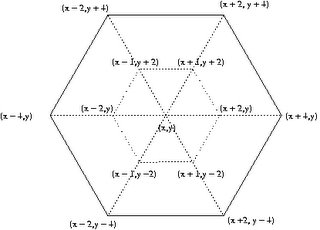
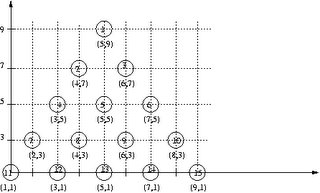
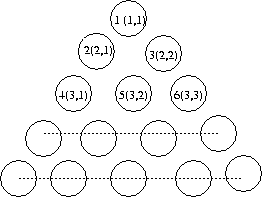
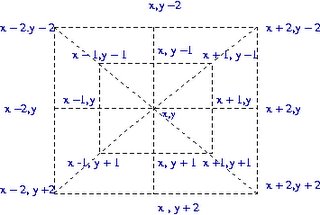
The explaination regarding what these bits mean now follows. The state of the triangular board is represented by using an unsigned 32 bit integer. The first (or the most significant) 17 bits are always zero since we use only the lower bits to represent the 15 pegs on the puzzle board. The least significant bit is zero if there is no peg in position 1 (refer to the board diagram in the previous blog) or it is set to 1 if there is a peg. Similar the the 2nd least significant bit is zero if there is no peg in position 2 or else it is set to 1.

Correct coordinate assignment and movement for the peg puzzle

Peg Puzzle Solution Design is invalid

Just realized that my approach to solving the peg puzzle solution is invalid. Basically the co-ordinate assignment and the movements are wrong. Will be posting the correct approach pretty soon, so stay tuned!!!

Computer Puzzles

Click here

Access Control Lists in Linux

Click here

Peg Coordinates and possible moves

The Cracker Barrel Peg Puzzle

I am planning to write a C/C++ program to solve the "Peg Puzzle" which is present on the dining tables at the Cracker Barrel restuarants. The puzzle is as follows

The puzzle consists of a triangular block of wood containing 15 holes, 14 of which have golf tees (aka pegs) in them. The game consists of jumping pegs over one another and removing the jumped-over peg, in a similar manner to checkers. The object is to end up with as few pegs as possible, hopefully one.

MSN Encarta - 6 Strange Secrets for Success

Click here

WEP: Dead Again, Part 1

Click here